大家好,我是小梁!
今天和大家分享下一种实用且常见的算法:Floyd判圈算法(Floyd Cycle Detection Algorithm),又称龟兔赛跑算法(Tortoise and Hare Algorithm)。
FLody判圈算法在链表上的应用有如下三种:
- 检测是否存在环
- 若环存在,可以计算出环的长度
- 若环存在,可以计算出环的起点
一.算法原理证明
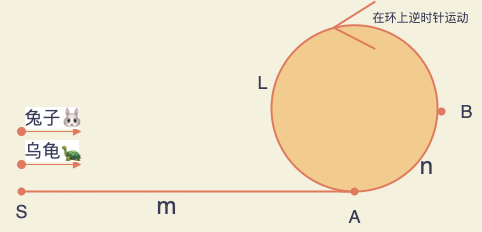
如图1 已知兔子和乌龟
- 同时从链表起点S出发
- 兔子速度是乌龟的两倍(乌龟每次向后移动1步,兔子移动每次向后移动2步)
- m是S和A之间的距离
- n是A和B之间的距离
- A是环的起点
- L是环的长度
- B是兔子、乌龟第一次相遇的点。
1.环是否存在
结论:若兔子在达到链表尾部前,乌龟与兔子相遇了,则说明链表有环。
反证法:若环不存在,那么乌龟永远追不上兔子,那么在兔子到达链表尾部前乌龟不会和兔子相遇。若相遇了,则链表有环。
2.求环的长度
已知乌龟和兔子相遇时,它们必定都在环上。设它们第一次相遇在B点,相遇后兔子保持不动,乌龟保持每次移动一步的速度继续前行,第二次相遇时,环长度L=第一次相遇后到第二次相遇时乌龟走过的路程。
3.求环的起点
设乌龟走过的全部路程为i,那么有
i = m + n + aL (1)「a是乌龟绕过的环的圈数」
因为兔子的速度是乌龟的两倍,所以有
2i = m + n + bL(2)「b是兔子绕过的环的圈数」
(2) – (1)可得:
i = (b – a)L (3)
结合式子(1)、(3)可得 m + n + aL = (b – a)L,所以有
m + n = (b-2a)L(4){因为m+n>0且L>0, 所以b-2a>=1}
所以可以得出结论:
m + n = 环长度L的正整数倍。(5)
当乌龟和兔子在B点第一次相遇后,让乌龟回到起点S,兔子仍在B,乌龟以每次1步的速度向前走,兔子以相同的速度绕环逆时针前进。当走了m步时,兔子和乌龟都正好在A处,即环的起点。因为兔子相对于A点走了(n+m)步,由结论(5)可知A必然是环的起点。
二.举一反三
知道floyd判圈法的原理后,我们来活学活用吧!请看题:
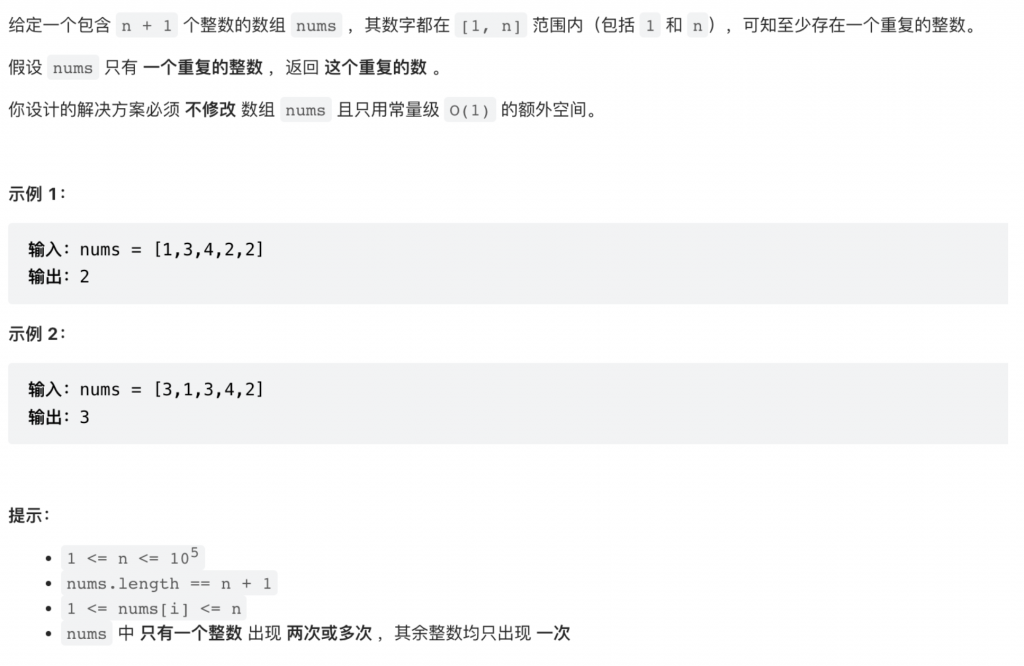
首先明确前提,整数的数组 nums 中的数字范围是 [1,n]。考虑一下两种情况:
如果数组中没有重复的数,以数组 [1,3,4,2]为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n), 其映射关系 n->f(n)为: 0->1 1->3 2->4 3->2 我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。这样可以产生一个类似链表一样的序列。 0->1->3->2->4->null
如果数组中有重复的数,以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n), 其映射关系 n->f(n) 为: 0->1 1->3 2->4 3->2 4->2 同样的,我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推产生一个类似链表一样的序列。 0->1->3->2->4->2->4->2->…… 这里 2->4 是一个循环,那么这个链表可以抽象为下图:
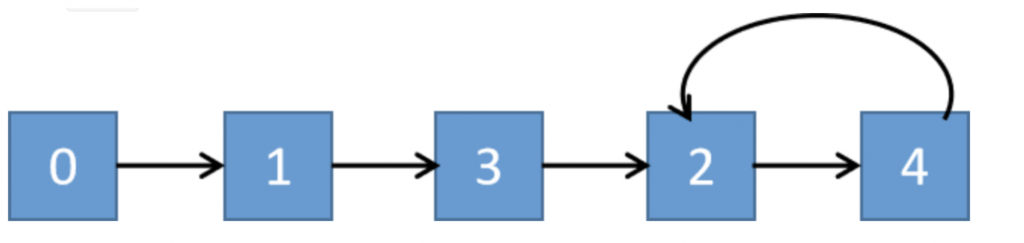
从理论上讲,数组中如果有重复的数,那么就会产生多对一的映射,这样,形成的链表就一定会有环路了,
综上,可以将问题转换成Floyd判圈算法
1.数组中有一个重复的整数 <==> 检测链表中是否存在环
2.找到数组中的重复数<==> 若环存在,可以计算出环的起点
下面是c++代码